Melakukan Uji Hipotesis dengan Nilai Variansi

Anda sedang membaca koran dan melihat informasi gaji profesi tukang bangunan. Koran ini menyatakan bahwa gaji per hari untuk tukang bangunan di kota Anda adalah sebesar Rp 113.000. Anda tertarik untuk membuktikan hal ini melalui Uji Hipotesis.

Anda mulai mengumpulkan data sampel gaji profesi tukang bangunan per hari. Anda telah menghitung nilai Mean dari himpunan data sampel itu, yang ternyata jumlahnya Rp 100.000, lalu nilai Standar Deviasi sebesar Rp 15.000, serta jumlah sampel sebanyak 30.

Hipotesis Null-nya adalah nilai Mean untuk gaji tukang bangunan per hari sebesar Rp 113.000. Maka Hipotesis Alternatif-nya adalah nilai Mean untuk gaji tukang bangunan per hari bukanlah Rp 113.000. Oleh karena itu, kita akan melakukan 2-sided test dalam Uji Hipotesis ini.

Pengujian diawali dengan melakukan standarisasi variabel lalu membandingkannya dengan nilai Critical Value of \( z \) atau Poin Kritis \( z \). Standarisasi variabel dilakukan untuk memperoleh \( Z \)-score.

Baca juga: Membangun Distribusi Normal Baku

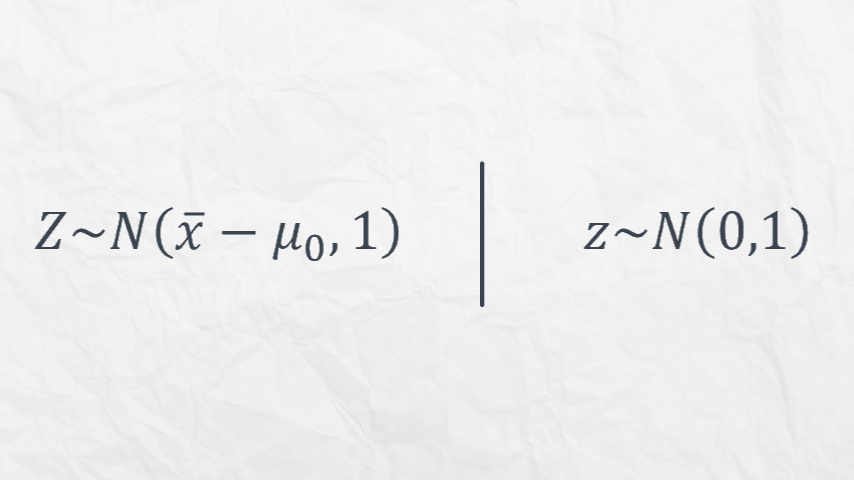
Nilai \( Z \) akan dibandingkan dengan nilai \( z \). Nilai \( Z \) adalah Distribusi Normal dengan nilai Mean \( \bar{x}-\mu_0 \) dan Standar Deviasi sebesar \( 1 \), sedangkan nilai \( z \) adalah Distribusi Normal dengan nilai Mean sebesar \( 0 \) dan Standar Deviasi sebesar \( 1 \). Kita akan berfokus dengan nilai Mean dari keduanya. Jika selisih nilai Mean dari \( Z \) dan \( z \) semakin kecil, maka semakin besar kemungkinan untuk menerima Hipotesis Null.

Kita akan mulai menghitung nilai \( Z \)-score.

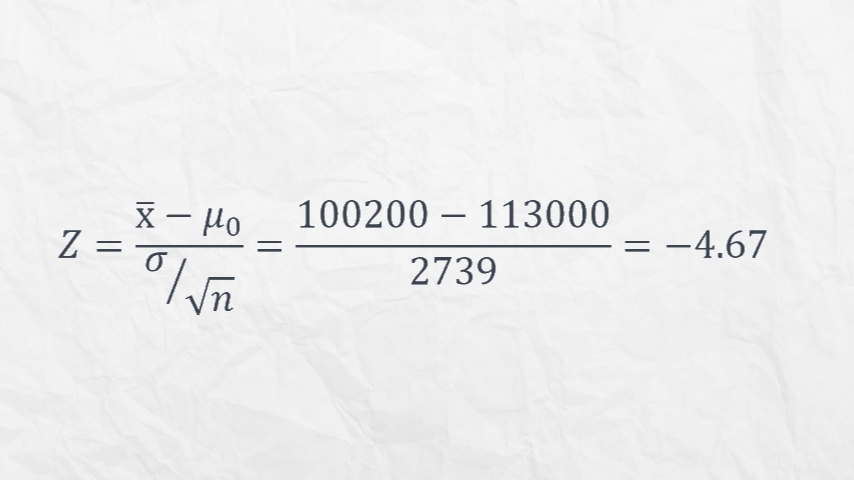
Nilai \( Z \)-score yang diperoleh adalah sebesar \( -4.67 \). Kita lanjut menghitung nilai Point Kritis \( z \).

Kita akan menggunakan nilai Significance Level sebesar \( 5\% \), sehingga \( \alpha \) sebesar \( 0.05\). Karena pengujian kita adalah 2-sided test, maka nilai alpha yang kita amati di z-table adalah sebesar \( 0.025 \), sehingga kita memperoleh nilai Poin Kritis \( z \) sebesar \( 1.96 \).

Sekarang waktunya kita membandingkan \( Z \)-score dengan Poin Kritis \( z \). Jika nilai \( Z \)-score lebih besar dari Poin Kritis \( z \) maka kita akan menolak Hipotesis Null. Nilai \( Z \)-score sebesar \( 4.67 \) (nilai ini menjadi nilai absolut, sehingga negatif menjadi positif) dan Poin Kritis \( z \) sebesar \( 1.96 \), maka kita menolak Hipotesis Null.

Penulis

Rachmat Wahid Saleh Insani adalah seorang Dosen di Bidang Ilmu Komputer. Ia bergelar Master of Computer Science dari Universitas Gadjah Mada.